Loading... ## 前言 对于十进制的整数使用二进制表示很简单，但是对于十进制小数如何使用二进制进行存储？十进制的小数又何如使用二进制小数表示？此文章描述了如何将十进制小数转换为二进制小数以及浮点数再内存中时如何进行存储。 ## 二进制小数 在计算机中，无论什么数据，最终存储都为二进制，对于整数部分很容易表示，但是对于非整数则比较困难。例如，十进制数`0.125`可表示为二进制`0.001`，怎么得来的？简单的计算可以用`0.125`不断乘`2`，结果小于`1`将二进制位记为`0`，结果大于`1`时将二进制位记为`1`： ``` 0.125 * 2 = 0.25 二进制位记作 0 0.25 * 2 = 0.5 二进制位记作 0 0.5 * 2 = 1 二进制位记作 1 ``` 所以得出结果为`0.001` > 另外可以把可以把十进制数`0.125`看做`1/2/2/2 = 1*2^-3`，十进制`1`换算为二进制还为`1`，二进制的负指数则相当于二进制数`1`右移位，用`2`的指数记为`2^-3`。 上面的例子因为能够用`2`的指数表示，所以能够被二进制精确的表达，但是有些情况，则无法使用二进制准确表达，例如一个人尽皆知的例子：十进制数`0.1`如何使用二进制表达？你会发现你无法用`2`的指数去表达它，即使用我们上面的计算方法： ``` 0.1 * 2 = 0.2 二进制位记作 0 0.2 * 2 = 0.4 二进制位记作 0 0.4 * 2 = 0.8 二进制位记作 0 0.8 * 2 = 1.6 二进制位记作 1 0.6 * 2 = 1.2 二进制位记作 1 0.2 * 2 = 0.4 二进制位记作 0 0.4 * 2 = 0.8 二进制位记作 0 0.8 * 2 = 1.6 二进制位记作 1 ... ``` 你会发现，它会无穷无尽的循环`0.0001100110011...`，这便是为何无法使用二进制数精确表达十进制小数。类似于使用十进制数也无法精确表达`⅓`，永远是`0.33333333...`。 ## 浮点数 浮点数是相对于[定点数](https://en.wikipedia.org/wiki/Fixed-point_arithmetic)而言的。 十进制数`1234`用科学计数法可写作：`1.234*10^3`，类似的，可用二进制表示为`0.10011010010*2^11`，我们称`10011010010`为尾数(mantissa/fraction)，`2`称为基数(Radix)，`11`则称之为指数(Exponent)。如此，小数点的位置根据指数的不同而浮动，称为浮点数。 那么在内存中，是如何使用二进制表示小数？[IEEE_754](https://en.wikipedia.org/wiki/IEEE_754)对此进行了标准化。 ### 单精度浮点数(Float) 单精度浮点数的存储使用`32`位二进制数，最高位`31`是符号位，用来表示正负数，`23-30`存储指数，低位`0-22`存储尾数。 需要注意的是，指数位的存储有两种方式： * 一种为有符号整数，意为有`1`位用来存储是正指数还是负指数。 * 另外一种情况存储为无符号整数，使用指数偏移量来计算是正指数还是负指数，例如，单进度浮点数的指数偏移量为`127`，意味着所存储的指数需要减去`127`，得出的结果便是正确的指数。 另外关于尾数的存储，在`正规数`(normal numbers)的情况下，二进制小数的表示总是以`1.x`开头，例如二进制数`1001`会表示为`1.001*2^3`而不是`0.1001*2^4`或`0.01001*2^5`。这在存储时则可省略开头的`1`，上面的`1001`则可存储为`001`且指数为`3`。 我们看一个具体的例子：十进制数`0.15625`  ``` 符号(Sign)：0 指数(Exponent)：偏移量计算方法，实际上我们应当存储的是-3指数， 用偏移量则为 127 - 3 = 124 转换为二进制为 0111 1100 尾数(Fraction)：按照上面的十进制小数计算二进制小数得出0.00101 = 1.01 * 2^-3， 去除前导1和指数得出尾数 = 01 ``` ### 双精度浮点数(Double) 双精度浮点数的计算类似于单精度浮点数，只不过存储大了一倍，它使用`64`位二进制数进行存储，与单精度浮点数相似，最高位`63`是符号位，用来表示正负数，`52-62`存储指数，低位`0-51`存储尾数，它的指数偏移为`1023`。 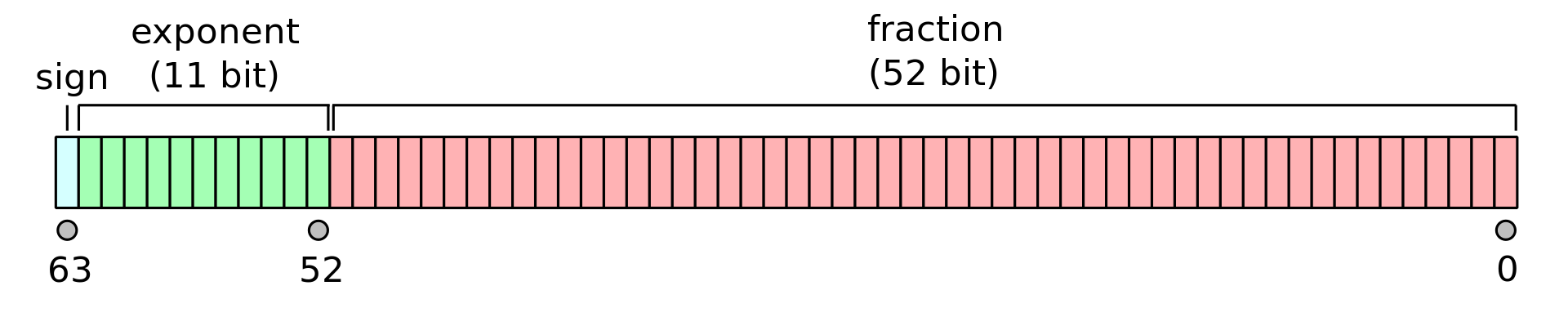 ### 其它值 无论是单精度还是双精度浮点数，都存在一些特殊的值，例如`次正规数`(subnormal numbers)和`0`以及`±无穷大`的数，还有无法正确转换的值`NaN`。 ## 结尾 精度越高的存储所需要的存储空间是越大的，当尾数过大无法存储时，根据[IEEE_754](https://en.wikipedia.org/wiki/IEEE_754)标准进行丢失精度的舍入。 # Reference * [IEEE_754](https://en.wikipedia.org/wiki/IEEE_754) * [Single-precision floating-point format](https://en.wikipedia.org/wiki/Single-precision_floating-point_format) * [Double-precision floating-point format](https://en.wikipedia.org/wiki/Double-precision_floating-point_format) * [Binary floating point and .NET](https://csharpindepth.com/Articles/FloatingPoint) * [How to get the sign, mantissa and exponent of a floating point number](https://stackoverflow.com/questions/15685181/how-to-get-the-sign-mantissa-and-exponent-of-a-floating-point-number) * [Floating point data types](https://www.trimble.com/OEM_ReceiverHelp/V4.44/en/FloatingPointDataTypes.html) * [Why do higher-precision floating point formats have so many exponent bits?](https://stackoverflow.com/questions/40775949/why-do-higher-precision-floating-point-formats-have-so-many-exponent-bits) * [浮点数](https://akaedu.github.io/book/ch14s04.html) * [How to convert float number to Binary?](https://stackoverflow.com/questions/3954498/how-to-convert-float-number-to-binary) * [IEEE-754 Floating Point Converter](https://www.h-schmidt.net/FloatConverter/IEEE754.html) 最后修改：2020 年 09 月 23 日 © 允许规范转载 赞 1 如果觉得我的文章对你有用，请随意赞赏
4 条评论
在说符号、指数、尾数那，那个横滑动栏实在是太难找了，找到了也好难滑动。希望博主能有空改进一下。。。 博客风格挺喜欢的OωO
这个滑动块我不好单独调整，我把内容换行，方便浏览
？？？
¿